개요

이 글은 퀵소트에 대해 정리한 글입니다.

퀵소트는 계속 까먹어서 책 ‘‘Hello coding 그림으로 개념을 이해하는 알고리즘’’ 으로 먼저 이해했다. 우선, 퀵소트=PARTITION이다.

이름에서 알 수 있듯이, 선택정렬 O(n²)보다 평균케이스가 O(nlogn)으로 훨씬 빠르다. 그 이유는 분할 정복 전략 덕분이다.

먼저, 분할 정복 전략을 위해 가장 간단한 기본단계를 구상해보자. 정렬하는데 가장 간단한 배열은 무엇일까?

잊지 말자! 아예 비어 있는 배열이나, 원소가 하나인 배열은 정렬할 필요가 없다! 그래서 기본단계이다. 그럼 재귀단계를 생각해보자. 퀵 정렬은 기준원소 pivot을 기준으로 배열을 나눈다. (partitioning)

분할을 하면 배열은 3개로 나뉜다.

• pivot보다 작은 숫자들로 이루어진 하위 배열
• pivot(기준원소)
• pivot보다 큰 숫자들로 이루어진 하위 배열

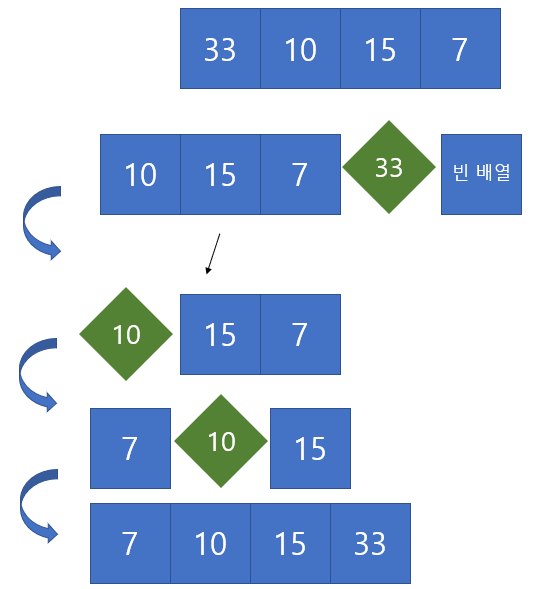위 그림에서 pivot은 33이고, 33보다 작은 숫자들로 이루어진 하위배열, 큰 숫자는 없으니 빈배열 이렇게 나눴다.

작은 숫자들로 이뤄진 하위배열 [10,15,7]에서 pivot을 10으로 잡고 다시 분할합니다. 분할 후, 분할된 하위 배열 [7]과 하위배열 [15] 그리고 pivot 10이 있다.

이를 통해 quick sort도 재귀함수임을 알 수 있다.

이를 코드로 구현하면 다음과 같다.

  def quicksort(array):
    if len(array)<2:
      return array
    else:
      pivot=array[0]
      less=[i for i in array[1:] if i <= pivot]
      # pivot보다 작은 하위배열
      greater=[i for i in array[1:] if i >= pivot ]
      #pivot보다 큰 하위 배열
      return quicksort(less)+[pivot]+quicksort(greater)

위의 코드는 pivot을 기준으로 대소비교한 뒤 작은 하위 배열, 큰 하위배열을 새로 만든다. 즉 메모리를 계속 사용한다는 뜻이다.

학교에서 배운 quick sort는 아예 주어진 배열에서, 새로 배열을 만들지 않고 partitioning을 한다. (신기하고.. 이해하는데 좀 시간 걸림 ㅋㅋ)

아래 사진을 첨부해놓았으니, 이해해보기를 바란다. (솔직히.. 첫번째 방법처럼 새로 하위 배열 만들어서 계속 재귀함수 돌리는게 더 쉽다.)

• 이 두 번째 퀵소트함수의 특징은 주어진 배열 내에서! 분할이 이뤄진다는 것이다. 새로운 배열을 만드는게 아님.

• 주어진 배열내에서 어떻게 분할하냐면, 작은숫자 하위배열의 마지막 idx 큰 숫자 하위배열의 마지막 idx를 swap해서 분할함.

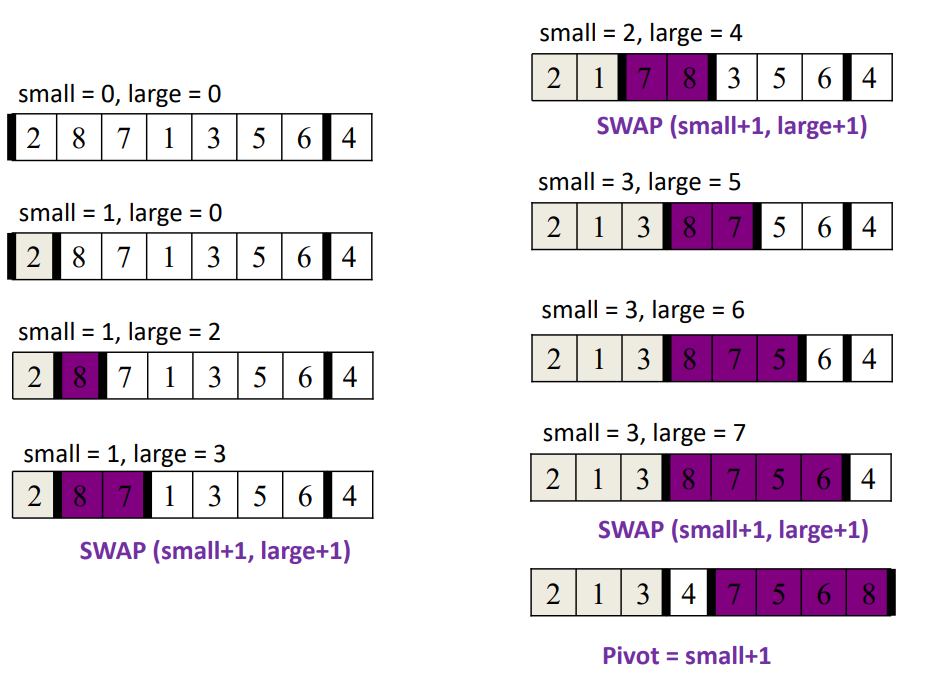
퀵소트는 pivot값을 랜덤하게 잡아야 average case가 O(nlogn)으로 수렴한다. 시험보기전 왜 그런지 읽어두기!!