[Algorithm]-1.삽입정렬과 선택정렬
in algorithms on Algorithms
개요
이 글은 삽입 정렬(Selection sort)과 선택 정렬(Selection Sort) 알고리즘에 대해 정리한 글입니다.
- 정렬 알고리즘
Insertion Sort
5,2,4,6,1,3이라는 리스트가 input으로 주어졌을때, inssertion을 이용하여 순서대로 1,2,3,4,5,6을 출력하는 알고리즘이다. 그렇다면 insertion(삽입)은 어떤 원리로 작동할까? 바로 key를 기준으로 대소비교를 통해 정렬된 리스트에 삽입을 하게 된다.
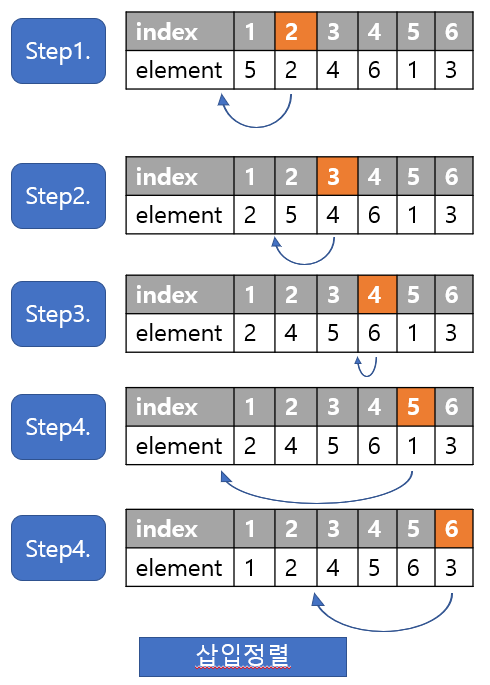
Step 1.에서 key은 두번째 원소 ‘2’다. key 2와 앞의 원소 5를 대소비교하면 2가 5보다 작으므로 2를 5앞으로 삽입한다.
Step 2.에서 key는 4이다. 4는 앞에 정렬된 리스트[2,5]와 대소비교시 2<4<5이므로, key인 4는 index=2 자리에 삽입한다.
Step3.에서는 key이 6이다. 앞에 정렬된 리스트[2,4,5]와 대소비교시 2<4<5<6이므로 index=4자리에 삽입한다.(즉, 그냥 그대로)
위에서 설명한 내용을 수도코드로 표현하면 아래와 같다. 
for문의 iteration은 input 리스트의 전체길이 n에서 첫번째 원소를 뺀 n-1만큼이다.(첫번재원소는 대소비교할 앞의 리스트가 존재하지 않기 때문이다.) 따라서 key는 index=2부터 시작하고, 앞에 원소와 비교하기 위해 앞의 원소 인덱스 i를 정의한다.
while문에서는 앞에 정렬된 리스트에서 key의 위치를 찾기 위해 i에서 1을 빼주며 이전 원소와 key를 비교한다.
예를 들어, 앞에 Step 2.에서 앞의 정렬된 리스트[2,5]와 key 4를 생각해보자. j=3이고 A[j]=4다. i=2(i=j-1)이고, A[2]=5다. A[2]>key이므로 while문을 돈다.
A[2+1]=A[2] 즉, index 3위치에 앞의 원소 5를 할당한다. (왜냐하믄, key가 정렬된 리스트의 마지막원소 5보다 작으니까 자리를 만들기 위해 마지막원소를 밀어주는 것임) 그리고 이제 i를 감소시켜주면 key와 원소 2를 비교함. 2는 key보다 작으므로 while문 탈출한다.(A[i]<key
원소2(i=1)의 앞자리인 i+1에 key값을 넣어준다.
시간 복잡도는 어떨까? 각 loop마다 드는 수행시간은 주어진 리스트가 정렬되었는지, 아닌지에 따라 best-case(O(n))와 worst-case((O(n²))로 나뉜다.
Selection Sort
쉬운 예제로 이해하자. 내 컴퓨터에 음악이 많이 저장되어 있다고 가정해본다. 가수별로 몇 곡을 들었는지 기록되어 있다.
이 목록을 가장 많이 들은 것부터 가장 적게 들은 것 순서대로 정렬하여 순위를 알고 싶다면 어떻게 해야할까?
선택정렬의 방법을 쓰면 다음과 같다.
- 리스트의 모든 항목을 살펴보고 가장 많이 연주된 가수를 찾는다.
- 새로운 리스트에 위의 Max값을 기록한다.
이를 그림으로 표현하게 다음과 같다.

컴퓨터공학을 공부하는 입장에서 시간복잡도를 계산해보자. 가수목록에서 가수를 한 명씩 찾아볼 때, 즉 연주 횟수가 가장 많은 가수를 찾기 위해서 목록의 모든 항목을 점검한다.
원본리스트 한 번 점검시 O(n)시간 만큼 걸리고, n개의 항목이 존재하니 n*O(n) = O(n²) 만큼의 시간이 걸린다.
